GARIS KUASA TERHADAP DUA LINGKARAN
Garis kuasa adalah suatu garis yang merupakan
tempat kedudukan titik-titik yang mempunyai
kuasa sama terhadap dua lingkaran.
BA = BC
PQ = PR
KL =KM
Persamaan Garis Kuasa
Untuk \(L_1 = x^2+y^2+A_1x+B_1y+C_1=0\) dan \(L_2 = x^2+y^2+A_2x+B_2y+C_2=0\) maka persamaan garis kuasa dirumuskan :
\((A_1-A_2)x+(B_1-B_2)y=0\)
garis kuasa dua lingkaran selalu tegak lurus dengan garis yang menghubungkan kedua pusat lingkaran
Misalkan f adalah garis kuasa dan D adalah nilai diskriminan persamaan kuadrat hasil substitusi f pada \(L_1\) dan \(L_2\)
D > 0 : lingkaran \(L_1\) dan \(L_2\) saling berpotongan.
(\r_1+r_2>P_1P_2\)
Misalkan f adalah garis kuasa dan D adalah nilai diskriminan persamaan kuadrat hasil substitusi f pada \(L_1\) dan \(L_2\)
D = 0 : lingkaran \(L_1\) dan \(L_2\) saling bersinggungan
Bersinnggungan Luar
(\r_1+r_2=P_1P_2\)
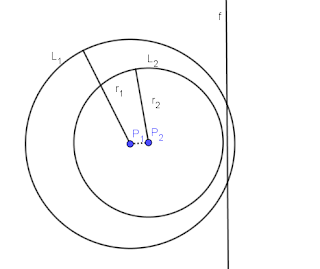
Bersinggungan Dalam
\(r_1+r_2>P_1P_2\)
D<0 : lingkaran \(L_1\) dan \(L_2\) saling lepas
Saling Lepas Luar
\(r_1+r_2<P_1P_2\)
Saling Lepas Dalam
\(r_1+r_2<P_1P_2\)






0 komentar